La distribuzione di Benford contro le truffe
14 Giugno 2013 La distribuzione di Benford, meglio nota come la legge della prima cifra, è una distribuzione probabilistica che descrive con quale probabilità, un numero presente in una raccolta di dati (p.es. popolazione dei comuni, quotazione delle azioni, costanti fisiche o matematiche, numero di strade esistenti nelle località) cominci con una determinata cifra.
La distribuzione di Benford, meglio nota come la legge della prima cifra, è una distribuzione probabilistica che descrive con quale probabilità, un numero presente in una raccolta di dati (p.es. popolazione dei comuni, quotazione delle azioni, costanti fisiche o matematiche, numero di strade esistenti nelle località) cominci con una determinata cifra.
A primo acchito sembrerebbe una affermazione stupida, e pare sia stata scoperta inizialmente dal matematico e astronomo Simon Newcomb (in foto) il quale la pubblicò nella rivista American Journal of Mathematics nel 1881.
Come tutti gli astronomi, Newcomb doveva fare tonnellate di calcoli numerici e sfruttava, come gli altri ricercatori, quella grande invenzione neperiana che erano le tavole dei logaritmi (con esse i calcoli, pur se appena più approssimativi, erano molto semplificati e si risparmiava molto tempo).
Fino all’avvento delle macchine calcolatrici, i logaritmi (o meglio le tavole logaritmiche e il regolo calcolatore) sono stati uno strumento essenziale ed estremamente usato per lo svolgimento di calcoli complessi.
Facciamo alcuni esempi:
– Per moltiplicare due numeri positivi era infatti sufficiente passare ai loro logaritmi, sommarli e poi tornare indietro (il vantaggio era che la somma è una operazione molto più agevole che dover calcolare il prodotto di più numeri con diversi decimali).
– Per fare il calcolo della radice n-esima di un numero positivo, bastava fare la divisione per n del suo logaritmo (anche qui la divisione era molto più semplice che calcolare la radice n-esima).
Sembra (ma non si sa se sia solo un aneddoto) che Newcomb (forse in un momento di ozio e fancazzismo) abbia notato delle anomalie nelle sue tabelle dei logaritmi, notò infatti che le pagine con le tabelle aventi 1 come prima cifra fossero molto più sporche delle altre, molto più del normale.
Sembrava che, nei sui calcoli, gli capitasse molto più spesso di cercare il logaritmo di un numero che iniziasse con una cifra bassa più che di una cifra alta.
Ricordo per chi è giovane e non ha mai avuto la necessità di consultare le tavole dei logaritmi, che per trovare il logaritmo di 42, di 42000 e e di 0,0042 si cerca sempre lo stesso elemento 4,2 perché le tavole riportano solo la parte decimale del logaritmo (la cosiddetta mantissa), mentre la parte intera la si ricava con un calcolo banale (da fare a mente).
Logicamente egli pensò che questo dipendeva dal fatto che le pagine con numero iniziale basso venivano usate molto più di frequente rispetto alle altre.
A queste affermazioni, apparentemente infondate, molti studiosi pensarono che vi fosse un errore di fondo, in quanto è ovvio che le pagine iniziali di un libro si sfoglino molto più di frequente rispetto a quelle di centro o di fondo perché normalmente chiunque parte dall’inizio per arrivare alla pagina che si cerca e, di conseguenza, sono giocoforza più usate e sporche.
Diceva: Che le dieci cifre non appaiono con uguale frequenza deve essere evidente a chiunque faccia molto uso delle tavole dei logaritmi, e noti che le prime pagine sono più consumate delle ultime. La prima cifra significativa è 1 più spesso che un’altra cifra, e la frequenza diminuisce fino al 9 …
La legge della probabilità dell’apparire dei numeri è tale che tutte le mantisse dei loro logaritmi sono equiprobabili.
Chi criticava aveva ovviamente la convinzione che la probabilità che un numero, scelto a caso, si presenti, seguirebbe la normale distribuzione statistica.
Un po’ come dire che, se si dispone di un dado non truccato e si fanno una quantità sufficientemente grande di tiri tale da normalizzare la distribuzione, si potrà riscontrare che la quantità di volte che esce l’1, il 2, il 3, il 4, il 5 o il 6, grossomodo si equivalgono (nel caso di 1000 tiri, dovrebbe presentarsi un 4 all’incirca 166 volte, quasi esattamente come un 1, un 6 e tutte le altre 4 facce del dado).
Questa strana distribuzione di Newcomb invece colpì la fantasia di Frank Benford, un fisico che lavorava per la compagnia elettrica e, nel 1938, si pose la fatidica ed infantile domanda: ma perché succede questo?.
Iniziò quindi a raccogliere una mole impressionante di dati su qualunque cosa gli capitasse sotto mano, quindi si mise a studiare la frequenza della prima cifra di questi numeri che aveva raccolto. Scoprì subito che, indipendentemente dal fatto che si trattasse di chilometri, di torte, di costanti fisiche, di abitanti o di numeri civici, la prima cifra di questi valori non era mai distribuita uniformemente, c’era sempre una incredibile maggioranza di numeri 1 ( i numeri 2 a loro confronto, ne erano solo poco più della metà).
La distribuzione di Benford descrive quindi la probabilità che un numero, presente in molte raccolte di dati reali, cominci con una determinata cifra. Se prendiamo ad esempio l’1 in prima cifra di una qualsiasi distribuzione di numeri riferita ad una raccolta omogenea di dati, dovrebbe aggirarsi sempre intorno al 30 % secondo questa formula:
P(n) = log_{10}(n+1) – log_{10}(n) = log_{10}(1+1/n)
Benford dopo aver postulate e diffuse le sue deduzioni non fu però in grado di spiegarne matematicamente il motivo, ma forse fu proprio per la sua dedizione al problema che si decise di intitolargli la legge.
Il problema della verificabilità della teoria di Benford si protrasse per molto tempo. Ci provò nel 1961 Roger Pinkham (matematico e statistico statunitense, professore presso la Rutgers University), ma riuscì a tirar fuori una dimostrazione un po’ arrangiata che rispondeva solo ad alcuni perché e tendenzialmente da un punto di vista logico.
Egli supponeva che si trattava di una invariante di scala (in fisica e matematica, l’invarianza di scala è una caratteristica degli oggetti o una legge che non cambia se si scalano le lunghezze di un fattore comune) e che doveva essere universale, sia che si misuri il prezzo del dollaro, delle dracme o le conchiglie della Nuova Guinea, sia che si applichi una unità di misura in centimetri, in cubiti o piedi.
La sua spiegazione logica sia pur breve e intuitiva era data dal fatto che noi contiamo sempre ad iniziare dal numero 1 e si va poi oltre fino al 9.
Se proviamo a pensare alle sole cifre da 1 a 9 è chiaro che abbiamo le stesse probabilità che una cifra inizi con 1 o 2 o 3 o 9. Se, però, prendiamo in considerazione i numeri da 1 a 20 ecco che oltre all’1, da 11 a 19 avremo molti più numeri che iniziano con la cifra 1. Se prendiamo quelli da 1 a 30 ne ho molti che iniziano con 1 ma anche con 2. Come si può facilmente notare, per avere numeri che inizino con 9, si dovrà andare molto in là con la numerazione e quindi aumenteranno anche la quantità di quei numeri che inizieranno con 1 o con 2 e quindi con cifre basse, per cui in una distribuzione di numeri legati a superfici, popolazioni, sarà più alta la probabilità di averne che iniziano con 1 piuttosto che con 9.
Alla fine è proprio nei tempi più recenti (nel 1996), che Theodore Preston Hill, uno statistico statunitense (detto Ted), dimostrò il teorema sulle distribuzioni miste in particolare la variabile casuale di Benford.
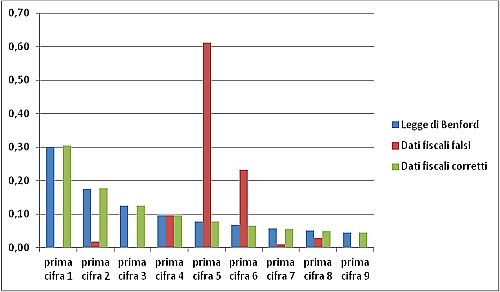
La cosa comunque singolare è che Benford già ai suoi tempi (e senza computer o macchine da calcolo), riuscì a far vedere che per moltissime distribuzioni, la probabilità che un numero inizi con una certa cifra tra 1 e 9 è quasi sempre la stessa (in particolare 30,1% per la cifra 1, 17,6% per la cifra 2 e via via fino al 9 con solo un misero 4,6% di presenza).
Applicazioni pratiche
Benchè sembrava trattarsi di una leggina piuttosto empirica, per la US Internal Revenue Service (gli uffici adibiti al controllo fiscale degli USA) non sembrava per nulla una banalità.
Prendiamo ad esempio una azienda fantasma creata esclusivamente per lo scopo di frode fiscale, mettiamola ora a generare qualche migliaio di fatture false e fittizie con importi casuali che vanno dai 100 ai 100000 € per poi inviare la documentazione all’Agenzia delle Entrate.
Ma che valori assegnare alle fatture? Benché vi fossero degli evasori molto scrupolosi, sappiamo che noi umani non siamo in grado di scrivere un gruppo di numeri davvero casuali, così andiamo sul sito random.org e ci facciamo generare 976 numeri distribuiti uniformemente in quell’intervallo (perché 976? Anche quel numero lo abbiamo scelto a caso tra 950 e 1050, proprio per non generare dei sospetti).
Ora sembrerebbe tutto a posto e a prova di bomba! Sì, forse in Italia sì, ma negli USA un tentativo di frode di questo tipo accadde davvero e fu sventato dall’agenzia delle tasse preposta. A quei tempi (ora non lo sappiamo), in quella agenzia, vi era il funzionario Mark Negrini www.negrini.com (chissà forse pure italiano) autore di alcuni libri sul tema, che dichiara:
L’applicazione della legge di Benford nella ricerca delle frodi può sembrare una pistola con un colpo solo, e sembra diventare inutile nel momento in cui la legge di Benford diventa conosciuta al grosso pubblico. In realtà la sua applicazione può variare in modalità e raffinatezza, rendendo comunque difficile la creazione di dati numerici falsi…
Il problema di quelli che commettono frodi è che, fino al momento in cui tutti i dati non sono inseriti, non si ha idea di come appariranno poi nel quadro complessivo.
Le frodi di solito riguardano una parte di un dataset, ma quelli che frodano non sanno come questo verrà analizzato, se per trimestre, per dipartimento o anche per regione. Verificare che la frode non violi la legge di Benford diventa allora molto più duro e difficoltoso, per non parlare del fatto che molti di quelli che frodano, non sono quasi mai ingegneri aerospaziali.
Un saluto