L'armonia della matematica frattale

Benoît Mandelbrot, nato a Varsavia nel 1924 (morto recentemente il 14 ottobre 2010), è stato il matematico padre della geometria frattale. Egli scoprì questa nuova branca di matematica quasi per caso nel 1979, mentre conduceva degli esperimenti per conto del Thomas J. Watson Research Center dell’IBM.

Un frattale è un oggetto geometrico che si ripete nella sua struttura allo stesso modo su scale diverse, cioè non cambia aspetto anche se visto con una lente d’ingrandimento (caratteristica chiamata auto similarità). Il termine frattale è un neologismo che venne coniato dallo stesso autore e deriva dal latino fractus (rotto, spezzato), per descrivere alcuni comportamenti matematici che sembravano avere un comportamento caotico; infatti questo genere di fenomeni nasce dalla definizione di curve od insiemi tramite funzioni o algoritmi ricorsivi. Per questa particolare natura, i frattali compaiono spesso nello studio dei sistemi dinamici e nella teoria del caos.

L’applicazione della geometria frattale a questioni economiche condusse Mandelbrot a rimettere in discussione alcuni solidi fondamenti dell’economia classica e della finanza moderna, quali l’ipotesi di razionalità dei comportamenti degli agenti economici, l’ipotesi dell’efficienza del mercato e quella secondo la quale i movimenti dei prezzi di mercato sono descrivibili come un cammino casuale. L’analisi frattale delle variabili economiche e finanziarie ha portato quindi alla nascita della cosiddetta finanza frattale.
La scoperta dei frattali in matematica, dimostrò che questa può essere la chiave di lettura delle forme casuali o caotiche presenti in natura, (alberi, montagne, nuvole, foglie, etc.), tutti caratterizzati da una forma ed un carattere irregolare e non potevano essere studiati usando la tradizionale geometria euclidea (fatta di rette, poligoni o cerchi).

Da alcuni fu definita “meraviglie senza fine che saltano fuori da semplici regole, che vengono ripetute all’infinito“.

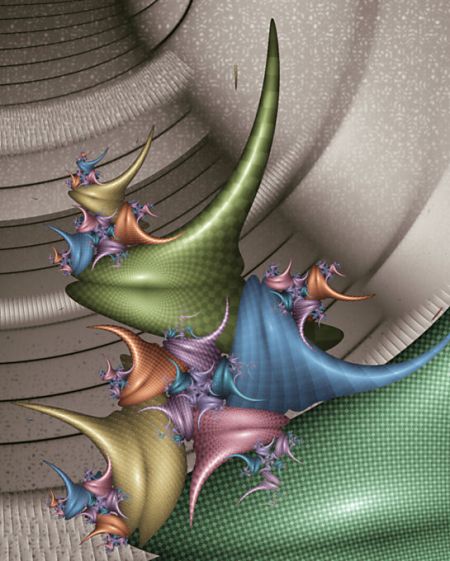
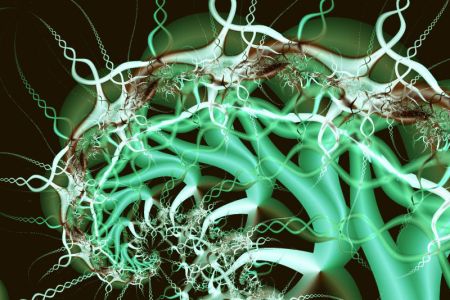
Noi qui non ci addentreremo sulla teoria né sulle matematiche (pur semplici) che la regolano, vogliamo solo presentarvi cosa può creare questa tecnica applicata nelle forme e nei colori della computergrafica. Vedrete forme armoniose e colori sfumati che sembrano quasi naturali senza alcun ausilio di pittori, ma solo di una innovativa e semplice sequenza di formule matematiche.
Tutti i frattali che vi riporto sono tratti da frattali.net un enorme catalogo on line dei più belli frattali mai calcolati. Prima però un filmato introduttivo.