La storia del Pi greco
11 Marzo 2011
Per chi non lo sapesse, il Pi greco (![]() ) non è altro che il numero che si ottiene dividendo la circonferenza di un cerchio per il suo diametro (o, anche, il valore dell’area di un cerchio di raggio unitario).
) non è altro che il numero che si ottiene dividendo la circonferenza di un cerchio per il suo diametro (o, anche, il valore dell’area di un cerchio di raggio unitario).
Il Pi greco è conosciuto come la costante di Archimede o di Ludolph ed è stato considerato dai matematici della storia un numero strano ed affascinante tanto che molti ci hanno speso una intera vita per calcolarlo con la più alta precisione possibile.
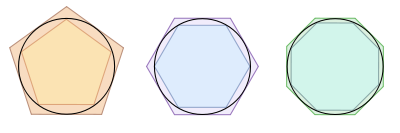
L’impossibilità di quadrare un cerchio (diventato anche un modo di dire) viene dimostrato empiricamente dal semplice metodo di calcolo di Archimede (in figura) utilizzando dei poligoni (nel 200 a.C.) e successivamente, oltre 2000 anni dopo, da Johann Heinrich Lambert (nel 1761) e da Ferdinand von Lindemann (nel 1882).
Il Pi greco è quindi una costante matematica e irrazionale che, a causa della sua natura trascendente, non possiede espressioni semplici e finite che la possono rappresentare. Di conseguenza il suo calcolo viene fatto esclusivamente con calcoli numerici per approssimazioni successive.
In molti casi il suo valore 3,14 è sufficiente, ma per maggior precisione molti lo usano con 4 decimali (3,1416) e alri ancora con 5 decimali (3,14159).
Un pignolo potrebbe usare molte cifre in più (per pura dimostrazione di saccenza), ma ai fini pratici poco cambia sui risultati finali. Vi mostro un esempio di un Pi greco con 999 cifre decimali
97494459230781640628620899862803482534211706798214808651
32823066470938446095505822317253594081284811174502841027
01938521105559644622948954930381964428810975665933446128
47564823378678316527120190914564856692346034861045432664
82133936072602491412737245870066063155881748815209209628
29254091715364367892590360011330530548820466521384146951
94151160943305727036575959195309218611738193261179310511
85480744623799627495673518857527248912279381830119491298
33673362440656643086021394946395224737190702179860943702
77053921717629317675238467481846766940513200056812714526
35608277857713427577896091736371787214684409012249534301
46549585371050792279689258923542019956112129021960864034
41815981362977477130996051870721134999999837297804995105
97317328160963185950244594553469083026425223082533446850
35261931188171010003137838752886587533208381420617177669
14730359825349042875546873115956286388235378759375195778
185778053217122680661300192787661119590921642019… ecc. ecc.
potremmo continuare con molte altre cifre senza mostrare mai alcuna forma di regolarità.
– La storia racconta che uno scriba egizio di nome Ahmes che è lo scrittore del più antico testo conosciuto contenente una approssimazione del Pi greco,(siamo al XVII secolo a.C.) e ne descrive il valore come rapporto 256/81 (circa 3,160).
– Archimede di Siracusa (già citato) elaborò un metodo per approssimazioni successive piuttosto buono e preciso e lo usò per dimostrare che il Pi greco è compreso tra 223/71 e 22/7 (la media dei due valori è circa 3,1419).
– Il matematico cinese Liu Hui (nel 263 a.C.) calcolò il Pi greco come 3,141014 (preciso fino alla terza cifra decimale) e suggerì che 3,14 era già una buona approssimazione.
– Il matematico ed astronomo cinese Zu Chongzhi (nel V secolo) calcolò Pi greco compreso fra 3,1415926 e 3,1415927 e diede due approssimazioni: 355/113 e 22/7 (ottima precisione… ‘sti cinesi!).
– Il matematico ed astronomo iraniano Ghiyath al-Din Jamshid Mas’ud al-Kashi (1350-1439) ne calcolò le prime 9 cifre con un calcolo a base diversa dal nostro e ne ottenne la equivalenza precisa fino all’ultima cifra 2 Pi greco = 6,2831853071795865
– Il matematico tedesco Ludolph van Ceulen (1600 circa) calcolò i primi 35 decimali (era così orgoglioso del suo risultato che lo fece scrivere pure sulla sua lapide).
– Il matematico sloveno Jurij Vega (nel 1789) calcolò le prime 140 cifre decimali, di cui le prime 137 erano effettivamente corrette. Egli mantenne il record mondiale per oltre 52 anni, fin quando, nel 1841, William Rutherford calcolò ben 208 cifre decimali di cui le prime 152 erano corrette.
Approssimazioni tanto precise (oltre le 20 cifre dopo la virgola) in realtà non sono utilizzate da nessuno e non hanno alcuno scopo pratico (per darvi una idea dell’inutilità, potremmo voler pesare una nave intera e, per averne un valore più esatto, andiamo a rimuovere la polvere dal comodino dalla cabina del capitano! Pensate cambi qualcosa?).
Spesso il calcolo così estremizzato del valore del Pi greco si usa per provare le prestazioni di nuovi supercomputer, per fare analisi statistiche sulle sue cifre o per un uso tutt’altro che matematico (come vedremo più avanti).
Sta di fatto che, con l’avvento di macchine da calcolo meccaniche, poi elettroniche, fino ai computer, la gara del calcolo di un Pi greco sempre più preciso ancora procede e forse non terminerà nemmeno per questo secolo…

Tralasciando le meno significative, queste alcune “prestazioni” salienti riferite al periodo più recente:
1947 – D.F.Ferguson: calcola 620 cifre decimali, stesso anno ritenta e calcola 710 cifre decimali, poi ancora 808 cifre decimali utilizzando sempre una calcolatrice meccanica da tavolo (pensate poi al dito!).
1949